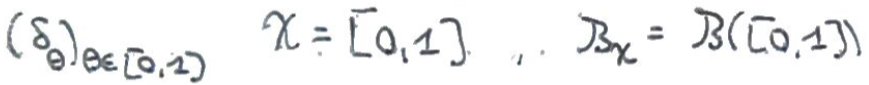Modèle statistique dominé \((\Omega,\mathcal A,({\Bbb P}_\theta)_{\theta\in\Theta})\)
Modèle statistique tel que toutes les \({\Bbb P}_\theta\) sont absolument continues par rapport à une Mesure sigma-finie \(m\) :$$\forall\theta\in\Theta,\quad{\Bbb P}_\theta\ll m.$$

• on dit que \(m\) est une domination (ou dominante) de \((\Omega,\mathcal A,({\Bbb P}_\theta)_{\theta\in\Theta})\)
• on peut toujours se ramener à une domination \(\tilde m\) qui est une Mesure de probabilité

Questions de cours

Démontrer :

Dans la définition de \(\sigma\)-finie, on peut supposer qu'aucun élément de la suite est négligeable pour \(m\).

Un certain rescaling fonctionne alors.

START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple simple de modèle statistique qui n'est pas dominé.
Verso:

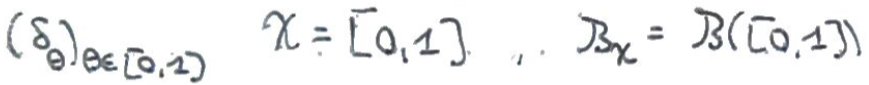
Bonus: (Masse de Dirac)
Carte inversée ?:
END